Ejercicio Resuelto. $$\iiint_\Omega y e^{-(x^2 + y^2 +z^2)^2} \mathrm{d}V$$ , con $\Omega := \{(x,y,z)\in \mathbb{R}^3 : x^2 + y^2 +z^2 \leq 1, y>0 \}$
La región a considerar es la siguiente:
Al tratarse de una región no parabólica contenida en una esfera, conviene un cambio a coordenadas esféricas (además, es mansito para la función que tenemos como integrando). Haciendo:$$x=\rho \cos \theta \sin \varphi \quad y = \rho \sin \theta \sin \varphi \quad z= \rho \cos \varphi \Longrightarrow \det J\varphi = \rho^2 \sin \varphi$$
Al tratarse de una región no parabólica contenida en una esfera, conviene un cambio a coordenadas esféricas (además, es mansito para la función que tenemos como integrando). Haciendo:$$x=\rho \cos \theta \sin \varphi \quad y = \rho \sin \theta \sin \varphi \quad z= \rho \cos \varphi \Longrightarrow \det J\varphi = \rho^2 \sin \varphi$$
, recorremos: $\rho \in [0,1], \varphi \in [0,\pi], \theta \in [0,\pi]$. Por tanto:
$$\begin{eqnarray} \iiint_\Omega y e^{-(x^2 + y^2 +z^2)^2} & = & \int_0 ^\pi \int_0 ^\pi \int_0 ^1 \rho \sin \theta \sin \varphi \cdot e^{-\rho ^4} \cdot \rho^2 \sin \varphi \ \mathrm{d}\rho \mathrm{d}\varphi \mathrm{d}\theta = \nonumber \\ & = & \int_0 ^\pi \sin \theta \mathrm{d}\theta \int_0 ^\pi \sin^2 \varphi \mathrm{d} \varphi \int_0 ^1 \rho^3 e^{-\rho^4} \mathrm{d}\rho =\frac{\pi (e-1)}{4e} \end{eqnarray}$$
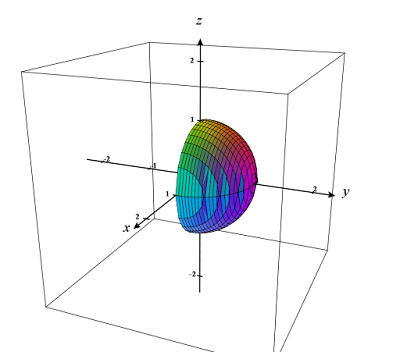
Comments