A familiarizarse con la definición de límite

El concepto de límite es uno de los más importantes en el cálculo diferencial, pues introduce y da pie a muchísimas ramas del análisis en una y varias variables. Es por ello que entender su definición es muy relevante a la hora de cualquier tipo de formalidad y entender propiamente los conceptos. La definición principal es la siguiente:

(Definición, límite)

$$\lim_{x\to a} f(x) = L \underset{\mathrm{Def}}{\Longleftrightarrow} \forall \varepsilon >0, \exists \delta = \delta(\varepsilon) >0: 0<|x-a|<\delta \Rightarrow |f(x)-L|<\varepsilon$$

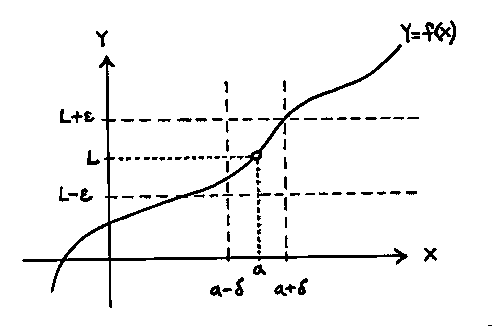
Para poder interpretar está definición correctamente, trataremos su entendimiento a partir de la siguiente gráfica: 

El concepto de límite viene dado a partir de la idea de proximidad. En concreto, si los valores de $f$ se acercan a un $L$ dado a medida que $x\to a$: deberíamos encontrar un entorno del punto $x=a$ (de amplitud $2\delta$) de forma que la distancia de las imágenes de $f$ respecto al supuesto límite, en dicho entorno ($0<|x-a|<\delta$), se achique tanto como uno quiera ($|f(x)-L|<\varepsilon$, siendo $\varepsilon >0$). Evidentemente, el entorno en cuestión dependerá de cuan próximo queremos las imágenes del $L$ en la definición (en otras palabras, $\delta$ depende de $\varepsilon$, y lo escribimos como $\delta = \delta(\varepsilon)$). Una vez entendida la definición, nos podemos lanzar a probar algún que otro límite:

Ejemplo: Probar $\displaystyle \lim_{x\to 2} \sqrt{x+2} =4$.

Queremos verificar:

$$\forall \varepsilon >0, \exists \delta(\varepsilon)>0: 0<|x-2|<\delta \Longrightarrow |\sqrt{x+2}-4|<\varepsilon$$

Sea $\varepsilon >0$, tenemos:

$$|\sqrt{x+2}-4|=\left | \frac{x-2}{\sqrt{x+2}+4} \right | = \frac{|x-2|}{\sqrt{x+2}+4}$$

Obsérvese que el numerador está acotado por $\delta$ a partir de la propia hipótesis planteada por la definición. Para trabajar el denominador, consideramos $\delta = 1$ inicialmente:

$$|x-2|<1 \Longleftrightarrow 1<x<3 \Longleftrightarrow \sqrt{3}+4 < \sqrt{x+2}+4 < \sqrt{5}+4 \color{brown} \Longrightarrow$$

Tomando inversos:

$$\color{brown} \Longrightarrow \frac{1}{\sqrt{3}+4} > \frac{1}{\sqrt{x+2}+4}$$

Obtenemos entonces:

$$|\sqrt{x+2}-4| < \frac{\delta}{\sqrt{3}+4}$$

Basta con tomar entonces $\delta = \min \{ 1,  (\sqrt{3}+4) \varepsilon \}$ para verificar:

$$0<|x-2|< \delta \Longrightarrow |\sqrt{x+2}-4| < \frac{\delta}{\sqrt{3}+4} \leq \frac{(\sqrt{3}+4)\varepsilon}{\sqrt{3}+4} = \varepsilon$$

Es importante resaltar el momento en el que tomamos un $\delta$ fijo para estimar una cota. Es un método viable pues el concepto de límite viene delimitado en cualquier vecindad del punto estudiado. En el ejemplo, al haber tomado $\delta =1$: trabajábamos el intervalo $(2-1, 2+1)\setminus \{2 \}$. Hay que tener cierto cuidado con la elección de este delta, pues debe ser tal que la expresión a acotar esté bien definida en el intervalo referido.

Ya que evidentemente no todos los límites en variable real residen en este caso, se requiere introducir las siguientes definiciones:

(Más definiciones)

$$\lim_{x\to a} f(x) = +\infty \underset{\mathrm{Def}}{\Longleftrightarrow} \forall K >0 , \exists \delta = \delta(K) > 0: 0<|x-a|<\delta \Longrightarrow f(x)>K$$

$$\lim_{x\to a} f(x) = -\infty \underset{\mathrm{Def}}{\Longleftrightarrow} \forall K>0 , \exists \delta = \delta(K)>0: 0<|x-a|<\delta \Longrightarrow f(x)<-K$$

$$\lim_{x\to +\infty} f(x) = L \underset{\mathrm{Def}}{\Longleftrightarrow} \forall \varepsilon >0 , \exists M= M(\varepsilon) >0: x > M \Rightarrow |f(x)-L|<\varepsilon$$

$$\lim_{x \to -\infty} f(x) = L \underset{\mathrm{Def}}{\Longleftrightarrow} \forall \varepsilon >0 , \exists M=M(\varepsilon) >0: x<-M \Rightarrow |f(x)-L|<\varepsilon$$

A la hora de trabajar con límites en el infinito, se procede exactamente igual que en sucesiones (límite por sucesiones).

Ejercicios:

1. Probar, haciendo uso de la definición de límite: $$\lim_{x\to 9} \frac{3x+13}{x+1} = 4$$ Ver solución.
2. Probar, haciendo uso de la definición oportuna de límite: $$\lim_{x\to +\infty} \frac{2^x +1}{3^x} =0 \qquad \lim_{x\to - \infty} \frac{\cos \left ( \frac{3}{2}x \right )x^2}{1+x^7} =0$$ Ver solución.

Anterior post - Siguiente post

Volver al artículo (Cálculo Diferencial de una variable real)